Parallel Computing with DNA

April 20, 2015

DNA. Everybody knows that DNA is the blueprint by which our cells replicate. Everybody knows that Horatio Caine uses it to catch bad guys. But… what if we used DNA to build supercomputers? That is definitely science-fiction… or is it? As I was working on DNA computing, I got my fair share of people staring at me like I was crazy. Someone even asked me if I could find a way to take a bird’s DNA to grow an optimal plane out of it. I thought I would demystify it a bit.

A bit of history

In 1994, Leonard Adleman (which you may know as the A in RSA) showed that it was possible to solve some pretty difficult problems, just by using DNA and other cell-reproduction related stuff. _Wait, what?_ Did he just recreate a Primordial-Soup-like environment, and waited until an organic supercomputer evolved from it, somehow following the rules of natural selection? Well, not exactly. But we’ll come to how things work in a minute.

DNA… but why?

It is important to understand the reasons why people came to study DNA Computing. The problem Adleman was trying to solve was really difficult. It is called the Hamiltonian Path Problem (but let’s call it The Roadtrip Problem), and it goes something like this:

• Take a map
• Cut out a part of the map, and you’ll be left with a few cities, linked by roads
• Grab a pen. Can you trace a path that goes through every city exactly once, following the roads?

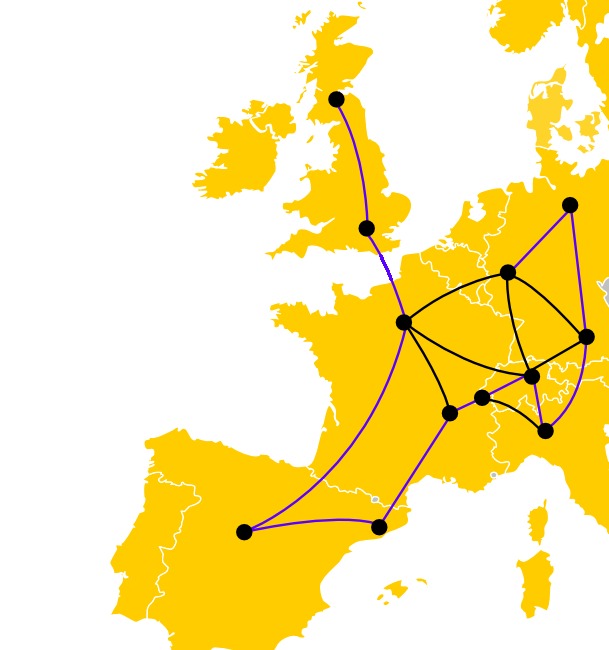
Roadtrip problem. Alright. The idea is this: the more cities you have, the longer it will take you to find out. And unfortunately, if you double the number of cities, you will probably need more than twice the amount of time to solve the new problem. And that means that if you just try every solution one after another, it is going to take an awful amount of time. Wouldn’t it be nice if you could try several of those possibilities at once?

This is basically the reason why computers nowadays have more that one core working at a time. It usually goes from two to eight, the latter more often than the former. Still, if a problem takes one year to be solved on a single core, using 8-cores instead would still take a month and a half. Not that cool if you need the results to do something else, huh? Well, that’s why super computers exist, hosting 250k+ cores. Your one-year-problem now takes about two minutes.

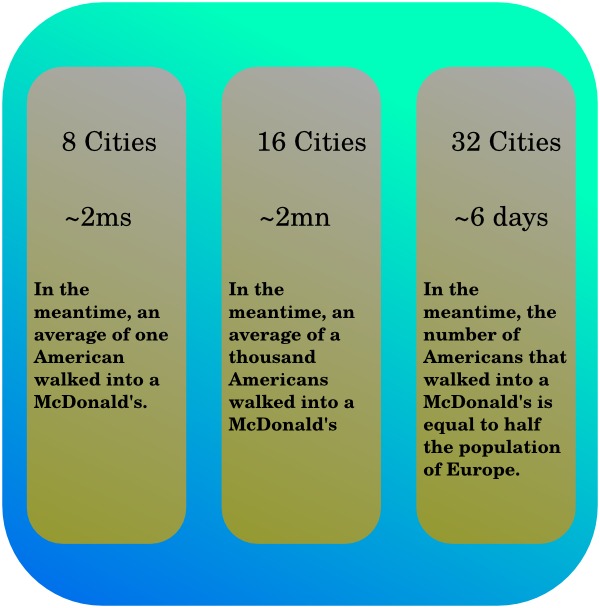Sometimes even that is not sufficient (which is kind of a good thing in regards to cryptography, for instance). One of the fastest algorithms for solving our roadtrip problem runs in $O(n^2 2^n)$. Basically that means that if a computer takes two thousandths of a second to solve the problem with eight cities, the same computer will need two minutes with sixteen cities, and a bit less than a week to compute a result for thirty-two cities. Most of that huge growth in time in regards of the number of cities comes from the exponential term $2^n$ , and the multiplication by $n^2$ does not help at all.

When scenarios like that show up, it drives some scientists mad, and sometimes gives them weird ideas. Among those is trying to solve NP-Complete problems with DNA.

DNA algorithms

DNA strands are like little strings (or sentences) containing information, in the form of four characters: A, T, C and G. It happens that the characters A and T attract each other, and the same goes for C and G (if like me you can never remember which goes with which, it’s very simple: Achilles and the Tortoise form a pair, and so do the Crab and his Genes). Characters of such pairs are called _complementary* to one another. If two DNA strands happen to contain sequences of complementary characters, they will attract each other, and clamp together, giving long DNA strands their sexy shape.

Now, let’s be serious, it’s 2015. And in 2015 you can design your DNA strands and have them produced. Let’s do exactly that (at least the design part). Bear with me for a minute, and imagine that we have our own DNA-strand-printer. Let’s design a simple DNA strand, containing a G character followed by 9 A characters:

GAAAAAAAAA

(a DNA strand, not somehow’s death throe)

Alright. Let’s call that strand N. Also, let’s print it two thousand times. Now let’s create an other strand. It is composed of 3 T characters, surrounded by a C and a G :

CTTTG

We’ll print that one… let’s say ten thousand times (by the way, DNA is very tiny). Those strands we call d. Now we’ll go to the kitchen, grab a bucket, fill it up with water, and throw our twelve thousand DNA strands in it. Congratulations, you just built and programmed your first DNA computer!

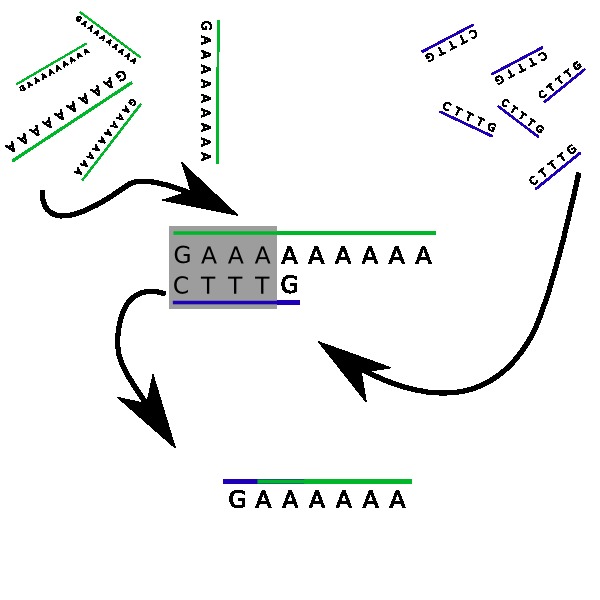
Let’s get that straight, right now: you won’t be running Minecraft on it anytime soon. But what exactly happens in the bucket? First of all, both strands contain complementary characters. The sequence TTT in d (our second strand) will tend to be attracted to any three As in our first DNA strand N. Yet, it can do even better: the first four characters of d, namely CTTT, are a perfect complement to the first four characters of N: GAAA. They will clamp together, and leave out two tails: a simple G on one side, and 6 As on the other side. Wait, this looks almost familiar…

Indeed, since DNA strands are flexible, the two tails will act as a new DNA strand GAAAAAA, which has the same structure as N, but with 6 As instead of nine. You see where this is heading: the process will repeat itself! Another d strand will float by, and its leading C character will get hooked. Every time this happens, the number of A characters on our main string will be reduced by three! Eventually, there won’t be any A left on our strand, all covered with Ts.

What we just implemented is a division of 9 by 3, effectively giving zero. The strand N encoded the number 9 with nine A characters, and the strand d encoded the subtraction by 3, with three T characters. This is easily extended to any numbers, can be used e.g. for checking if a number is prime or not. The truly amazing part is that all the computations are (almost) completely parallel: you have thousands of pairs forming, independently of others!

Of course, this is very theorethic, even though some succesful experimentation was done already. It is still the very beginning of DNA computing, and the time it takes to run an algorithm exceeds by far that of a computer (if you can run the given algorithm in a first place). Yet, it is promising, and in the end theoricists don’t care that much if it will work one day.

My contributions

Last February, I completed a research project as part of my Master’s studies. I was able to provide solutions to several problems using DNA algorithms, like:

• Checking if a number is prime
• Computing the square root of a number
• Implementing binary inputs for DNA problems

and also did some analysis on how fast/how reliable such algorithms were. The improvements compared to other DNA based computing are that

1. it is more scalable (at least theoretically)
2. it only uses DNA strands (Adleman, for instance, also used enzymes).

If you are hungry for DNA algorithm knowledge, have any questions, or want to complain about anything: just drop me a word in the comments below!

There are many problems (and solutions!) related to computing with DNA, and some of the following might be interesting to the reader:

• Adleman, L.M.: Molecular computation of solutions to combinatorial problems. In: Science Magazine. (November 2009)
• Zhang, D.Y., Winfree, E.: Control of dna strand displacement kinetics using toehold exchange. In: J A C S Articles. (June 2009)
• Qian, L., Winfree, E.: Scaling up digital circuit computation with dna strand displacement cascades. In: Science Magazine. (June 2011)

Also, Microsoft developed a tool for visualizing DNA computing. Have fun!